宮崎優のWebサイト

研究紹介

深層学習を用いた磁性金属の大規模シミュレーション

Mach. Learn.: Sci. Technol. 4, 045006 (2023)

磁性と金属が両立する系はよく知られていますが、その一方でその振る舞いは未だ完全に解明されたわけではなく、未踏の領域が広がっているとも言えます。 例えばスピンのダイナミクスランダウ＝リフシッツ＝ギルバート(LLG)方程式を解くことで調べられますが、計算コストの観点から伝導電子と相互作用する系のシミュレーションは最近まで行われてきませんでした。

そこで伝導電子の計算を深層学習で代替することで計算の高速化、大規模化を試みています。深層学習はGPUによる高速化や運動方程式を解くのに必要な自動微分を利用できるという点で相性がよく、近年注目されている機械学習ポテンシャルと類似した考え方と言えます。

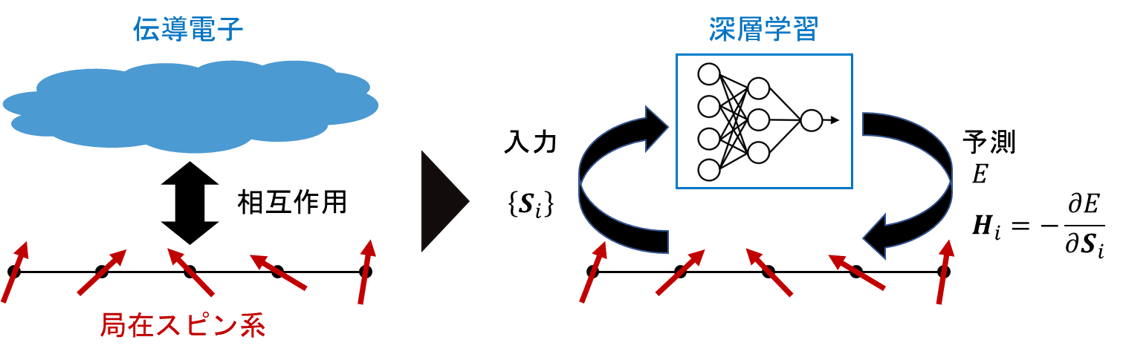
私の考案したアーキテクチャは近年深層学習分野で注目されている「同変性」を考慮したものとなっており、実際に既存のモデルよりも非常に高い精度を実現しています。実際に学習した深層学習モデルでダイナミクスを計算し、スキルミオンのような非常に複雑なスピン-電荷相互作用を持つ系を再現できることも確かめました。開発したパッケージはGitHub上でMITライセンスで公開されているので、どなたでも利用が可能です。

強磁性薄膜中のスキルミオンの表面弾性波を用いた駆動制御

Sci. Rep. 13, 1922 (2023)

スキルミオンは磁性体薄膜上のスピンが渦を巻いた構造をしており、そのトポロジーに由来する安定性や駆動に必要なエネルギーが非常に小さいことから、メモリやリザバー計算などへの応用が期待されていますが、実用化においてはいくつかの課題があります。

スキルミオンを駆動させる手法として電流を加えて伝導電子でスピンに力(トルク)を加えてスキルミオンを「押し出す」アプローチが主流ですが、電流をかけた方向と横方向にも動いてしまうスキルミオンホール効果と呼ばれる現象が実用化の1つの大きな課題となっています。

そこで本研究ではスキルミオンを薄膜内で自在に動かすことを目標としました。基板の歪み(表面弾性波)を利用し、スキルミオンを「閉じ込める」というアプローチです。これはイオントラップと呼ばれる装置と同じ原理を表面弾性波の重ね合わせで再現することでスキルミオンを閉じ込め、閉じ込め位置を動かすことでスキルミオンも追従します。

実際に数値計算で検証を行ったところ、ナノスケールで自在にスキルミオンを駆動させることが可能であることがわかりました。精密な駆動ができるだけでなく、単純なデバイス構造(ピエゾ基板上に強磁性体薄膜と4つのクシ型電極のみからなる)で実現可能な点や、スキルミオン位置を直接実験者が指定できる点に優位性があります。

トポロジカルナノワイヤ

Phys. Rev. Research 4, L022002 (2022)

近年、トポロジカル物性が基礎研究だけでなくスピントロニクスや量子計算などへの応用の観点からも注目されています。

特にトポロジカルディラック半金属はグラフェンの3次元版とも呼ばれる線形のバルクバンド分散(ディラックコーン)とスピン運動量ロックした特別な表面状態(フェルミアーク)を持ち、これらを反映した特異な輸送特性が予想されています。

このようなトポロジカル輸送特性を開拓するプラットフォームとして有力な候補の1つがCd₃As₂のナノワイヤです。Cd₃As₂ナノワイヤは

• 比表面積が大きい
• フェルミ準位が十分にディラック点に十分に近い

という非常によい特性を持つため、実際に様々なトポロジカル輸送特性が報告されています。

そこで本研究では化学気相成長(CVD)法でCd₃As₂ナノワイヤの合成と微細加工によるデバイス作製を行い、磁気輸送特性の評価を行ったところ、ナノワイヤに平行な磁場ではバルク由来のシュブニコフード・ハース(SdH)振動が観測された一方で、 垂直磁場ではバルクのSdH振動に加えて表面状態に起因すると考えられる量子振動が観測されました。ナノワイヤにおいて表面状態の量子振動は本研究において初めて観測されました。

SdH振動は固体中の電子状態を詳細に調べることができる強力なツールとして知られています。本研究はトポロジカルナノワイヤの表面状態を実験的に調査するプラットフォームを提供しています。

トポロジカルディラック半金属のナノワイヤの表面状態を用いてトポロジカル量子計算実現の要であるマヨラナ粒子を実現する理論的提案(参考)も報告されており、本研究ではトポロジカル量子計算の実現にも重要な貢献をしうると考えています。

methods

化学気相成長(CVD)法、電子線リソグラフィ、集束イオンビーム(FIB)法、透過型電子顕微鏡(TEM)

keywords

トポロジカルディラック半金属(TDSM)、ナノワイヤ、フェルミアーク、トポロジカル量子計算

ベイズ統計に基づいたインピーダンススペクトル解析

AIP Advances 10, 045231 (2020)

インピーダンススペクトルの解析は電気化学過程やイオン伝導過程の評価において重要な役割を果たしています。

特に2019年には私達が日常的に用いているリチウムイオン二次電池に関する研究についてノーベル化学賞が与えられたことや、燃料電池用の水素ステーションを街中で見かけるようになったことからも、電気化学反応を研究する重要性が増していることを実感いただけるのではないでしょうか。

インピーダンススペクトルの解析では電気化学反応の素過程を電気回路に置き換える等価回路モデルを求めます。具体的には交流測定で得られたスペクトル(ナイキスト線図)に現れる半円弧の数がRC並列回路の数に対応します(下図)。

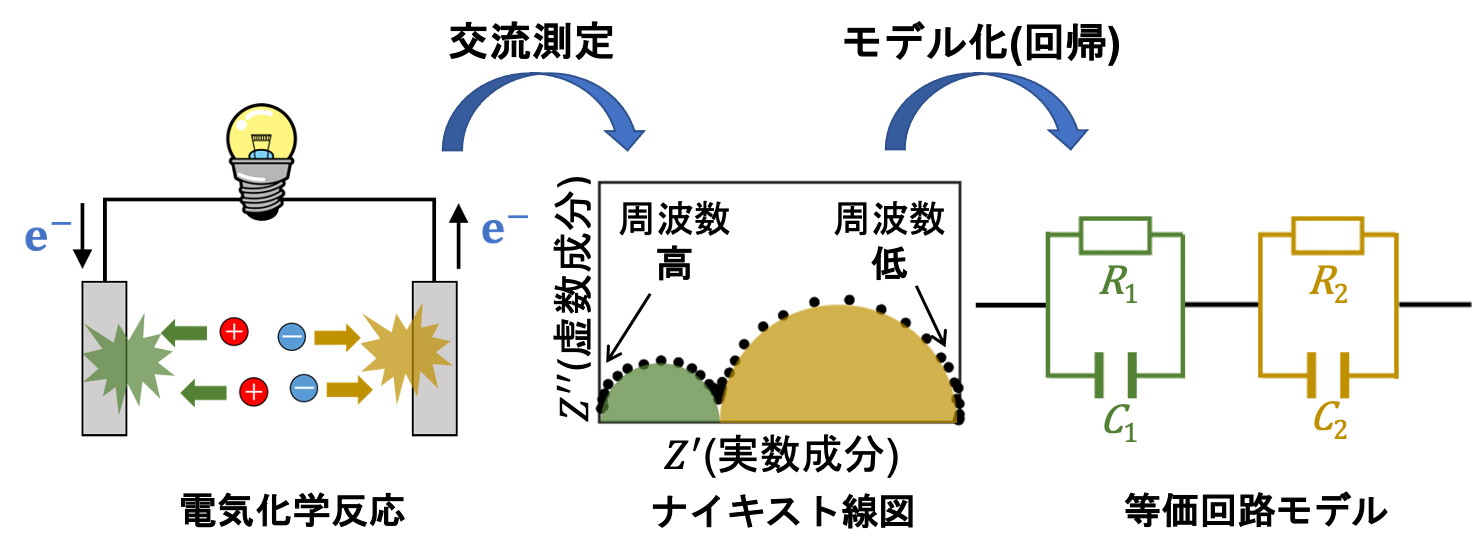
実際にはこのナイキスト線図を視覚的に判断して回路構造と初期パラメタを決定して回帰(非線形最小二乗法)を行うという方法で解析が行われています。

しかし、この方法にはいくつかの重大な問題点があります。まず、2つのRC並列回路について時定数$ \tau = RC $が近い場合、ナイキスト線図の半円弧の数は1つに見えてしまい、誤った回路構造で解析を行ってしまいます(下図)。

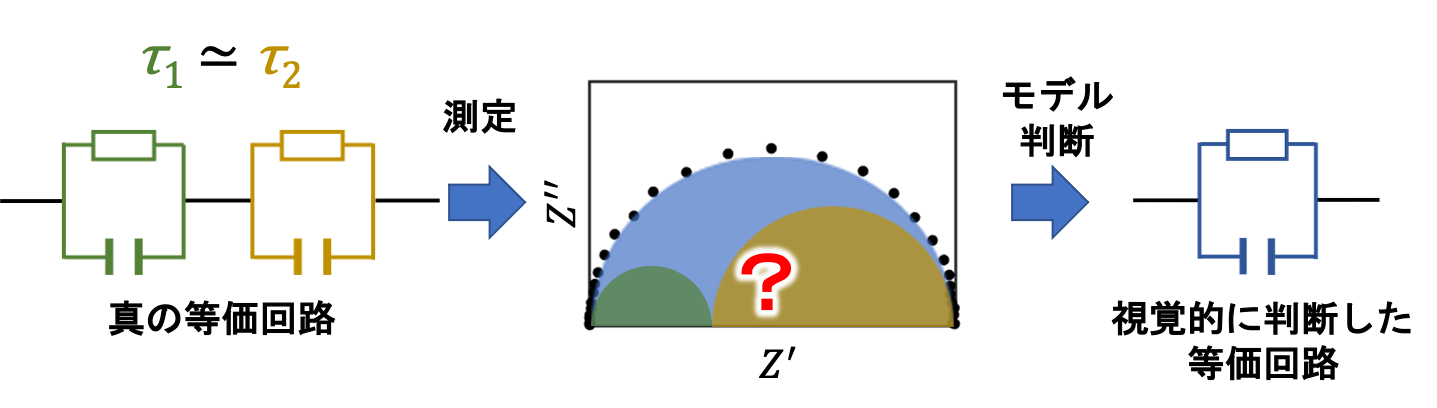
また、非線形最小二乗法は最小値ではなく極小値を求めるアルゴリズムのため、パラメタの初期値が適切でないとうまく機能しません。そのため、解析者が回路構造とパラメタの初期値を試行錯誤して、なんとなくうまくいっていそうなものを選んでいるというのが現状です。

そこで、本研究ではベイズ統計に基づいた解析(レプリカ交換法+WBIC)を提案し、スペクトルデータから正しい回路モデルを選択できるかという課題にアプローチしました。実際に人工データと実測データについて数値実験を行いました。

その結果、視覚的に判別が難しい場合であっても9割以上の確率で正しい回路モデルを選択できることがわかりました(具体的にどの程度時定数が近い場合まで正解できるのかも論文では議論されています)。

更に、パラメタの初期値をランダムに与えても解析がうまくいくことも実験的に示しました(下の註を参照)。

以上の結果は高精度なモデリングが可能なだけでなく、人間の手を介さずに解析が可能であることも意味しています。マテリアルズ・インフォマティクスにおいて、実験操作を自動化して大量にデータを収集するというアプローチが考えられていますが、実測データからどのように物性値を自動的に抽出するのかが重要な課題となっています。その意味で本研究の成果はマテリアルズ・インフォマティクスの加速に貢献しうると考えています。

methods

マルコフ連鎖モンテカルロ(MCMC)法、レプリカ交換法(交換モンテカルロ法、parallel tempering)、広く使えるベイズ情報量基準(WBIC)

keywords

ベイズ統計、電気化学、インピーダンススペクトル解析、マテリアルズ・インフォマティクス

(註：これは事後分布をサンプリングするアルゴリズムとしてレプリカ交換法を用いているためです。事後分布が多峰である場合、ベイズ統計でよく用いられるメトロポリス・ヘイスティング法やハミルトニアン・モンテカルロ法では収束が極端に遅くなってしまいます。同様の問題は統計物理学におけるスピングラス問題にも現れ、これを解決するために考案された手法がレプリカ交換法です。他にも工夫した点について色々と書きたいことはあるのですが、機械学習の雑誌ではないので本文に書けず......論文のsupplementary_materialに少しだけ書いてあります(何故WBICを用いたのかとか)。)

Mn_2-xCr_xSb反強磁性相における熱電効果の増大

J. Phys. Soc. Jpn. 89, 124601 (2020)

塩見研究室の仲川さんが中心となって行った実験の成果ですが、宮崎は密度汎関数法に基づいた第一原理計算を担当しました。計算と光電子分光法の双方の結果から、反強磁性相において現れるフェルミ準位付近の状態密度の巨大なピークが熱電性能の向上に寄与している可能性を示しました。

他にも(公開していないものも含めて)輸送特性(電気伝導、異常ホール効果、ゼーベック効果等)、バンド分散、磁気構造、最大局在ワニエ関数法を用いた有効模型の導出など、様々な第一原理計算の手法に精通しています。実験の研究をしていたという立場もふまえて、実験結果との整合性を重要視しています。

methods

密度汎関数理論(DFT)

keywords

磁性、熱電効果